一、题型说明
管理类联考数学的考试中有一类应用题,所给条件纷繁复杂,定量关系不明确,初学者常常不知所云,要求我们计算所花钱数最少或者时间最少或者果实最多,简而言之,就是要求我们建立模型实现利益最大化,我们把这类应用题叫做线性规划应用题。线性规划是运筹学中辅助人们进行科学管理的一种数学方法。在经济管理、交通运输、工农业生产等经济活动中,提高经济效果是人们不可缺少的要求,而提高经济效果一般通过两种途径:一是技术方面的改进,例如改善生产工艺,使用新设备和新型原材料;二是生产组织与计划的改进,即合理安排人力物力资源。线性规划所研究的是:在一定条件下,合理安排人力物力等资源,使经济效果达到最好。一般地,求线性目标函数在线性约束条件下的最大值或最小值的问题,统称为线性规划问题。这种题目的特点与管理类硕士学位对学生基本素养的要求有较高的契合度,因此近三年来受到出题老师的热衷,每年出一道题。而此类题通常是考生的软肋,这里文都教育管理类联考彭老师特意撰写此文,希望能在最后关头祝考生一臂之力。
二、历年真题及解析
1.(2013.1)有一批水果要装箱,一名熟练工单独装箱需要10天,每天报酬为200元;一名普通工单独装箱要15天,每天报酬为120元,由于场地限制,最多可同时安排12人装箱,若要求在一天内完成任务,则支付的最少报酬为( )
(A)1800元 (B)1840元 (C)1920元 (D)1960元 (E)2000元
答案:C
解析:本题中最多安排12人,可能为11人,也可能为10人,设安排熟练工
人,普通工
人
则有
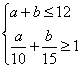
设
,则
,
设支付的报酬为
,则
当
取最大值6时,
取最小值,
2.(2012.1)某公司计划运送
台电视机和
台洗衣机下乡,现有两种货车,甲种货车每辆最多可载
台电视机和
台洗衣机,乙种货车每辆最多可载
台电视机和
台洗衣机,已知甲、乙两种货车的租金分别是每辆
元和
元,则最少的运费是( )元.
答案:B
解析:设需租用甲车
辆,乙车
辆,则有
设
,即
,则
运费
当
取最大值时,
取最小值,
3.(2010.1)某居民小区决定投资15万元修建停车位,据测算,修建一个室内车位的费用为5000元,修建一个室外车位的费用为1000元,考虑到实际因素,计划室外车位的数量不少于室内车位的2倍,也不多于室内车位的3倍,这笔投资最多可建车位的数量为( )
答案:B
解析:设建室内车位的数量为
,室外车位数量为
,则有
,令
,则
车位数量
,当
取最小值时,
取最大值,
4.(2010.10)某地区平均每天产生生活垃圾700吨,由甲,乙两个处理厂处理。甲厂每小时可处理垃圾55吨,所需费用为550元;乙厂每小时可处理垃圾45吨,所需费用为495元。如果该地区每天的垃圾处理费不能超过7370元,那么甲厂每天处理垃圾的时间至少需要( )小时
(A)6 (B)7 (C)8 (D)9 (E)10
答案:A
解析:设甲厂每天处理
小时,乙厂每天处理
小时,则
令
,则
,即甲厂最少需要处理6小时
三、解题方法总结
细心的同学可以观察到上面的四道题目我是用同一个方法解析的,总结起来可以分四步
一、根据题目限定条件列出不等式组
二、将第一个不等式设为等式代入第二个,求出其中一个未知数限定范围
三、写出目标函数并整理
四、根据未知数范围求解目标函数最值
各位考生可以看到,这类线性规划应用题,我并没有使用我们高中阶段学习过的方法,即在平面直角坐标系内绘出可行域,再进一步利用单纯形法求得目标函数在可行域内的最值,或者求得目标函数的取值范围,这样做的原因不外乎为了提高学生在考试中的解题速度,因为大家都知道,我们的考试不是会了知识就能得高分,要同时兼备速度与准确度才能在联考中立于不败之地,同时,大家根据以上四道真题完全可以毫不怀疑的相信,这种方法是可以解决联考中出现的所以线性规划应用题的。
除了解决这个题型,在这里我还得跟大家重点说几句,还有十几天考试就来临了,不要再追求多做几道题或者几套卷,如果你做的题目与真题没有很高的契合度,或者你总是用一种缓慢的方法无时间限制的做题,可以说你的工作完全无效,做题速度以及准确度,不是靠多做几道题能够实现的,靠的是对基础知识点极度熟练以及极度灵活的掌握,要求大家拿出真题,反复研磨真题中涉及的不太熟练的知识点,做到一个公式,无论从哪个角度出,都能够迅速反馈,而不是需要在纸上画半天才能得出需要的形式。另外,不要太在意模拟考试中的分数,模拟题有没有用,当然有用,但是他的用途不是判断你能在真正的考试中考出多少分,而是与真题的作用一样,判断你还有哪些知识点需要详细研磨,擅用模拟题,擅用真题,才能在考试中取得出其不意的效果。
最后,祝愿大家取得好的成绩,考上理想的院校,加油


























