一题：线性规划 

maxz=(4+θ)*x1+(12-2θ)*x2 s.t.X1+2*X2=10 2*X1+X2=10 0《θ《5 
根据θ的变化求最优值的变化。 
二：求线性规划的对偶规划。吴的书里好像有原题。最后约束条件是 -2《X1《5 a《X2《b 
X3，X4》0，X5无约束 
(记不清数字了）好像是原题 三：用对偶单纯形法求解 四：运输问题。

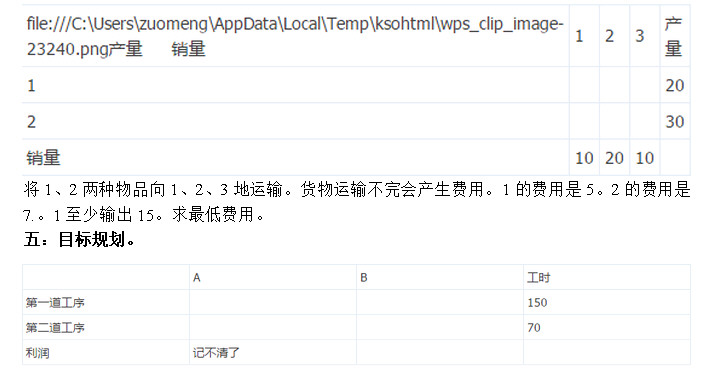
P1：利润不低于10000 P2：。。。。恰好等于 
P3：最大限度利用第二道工序，最好能能加班（这个记得不太全） 六：胡运权习题集上。设备更新问题。原题。 七：动态规划问题。 
Minz=∑Xk²（k=1......10）（求平方和）  
S.t X1*X2*X3.......X10=8(不会用求积符号) Xk>0.k=1,2....10 八：排队论、 
每个电话持续时间3分钟，每个人的忍耐限度为3分钟。 1能允许的最大通话量。 
2根据（1）求P0，Ls,Lq,Ws,Wq